在刷leetcode时有个求最长回文字符串的问题。

#官方题解提供了4中解决办法，分别是

1.暴力法， 2.动态规划， 3.中心扩展算法， 4.就是我们今天要介绍的Manacher方法。

在介绍算法之前，首先介绍一下什么是回文串，所谓回文串，简单来说就是正着读和反着读都是一样的字符串，比如”aba”，”上海自来水来自海上”等等，一个字符串的最长回文子串即为这个字符串的子串中，是回文串的最长的那个。

而Mnacher是最高效的算法，算法复杂度为O(n)。

Manacher算法原理与实现

Manacher算法提供了一种巧妙地办法，将长度为奇数的和偶数的回文串一起考虑，具体做法是，在原字符串两个字符中间插入一个分隔符#，同时在开头插入(@)，尾部也要添加一个分隔符（$）。

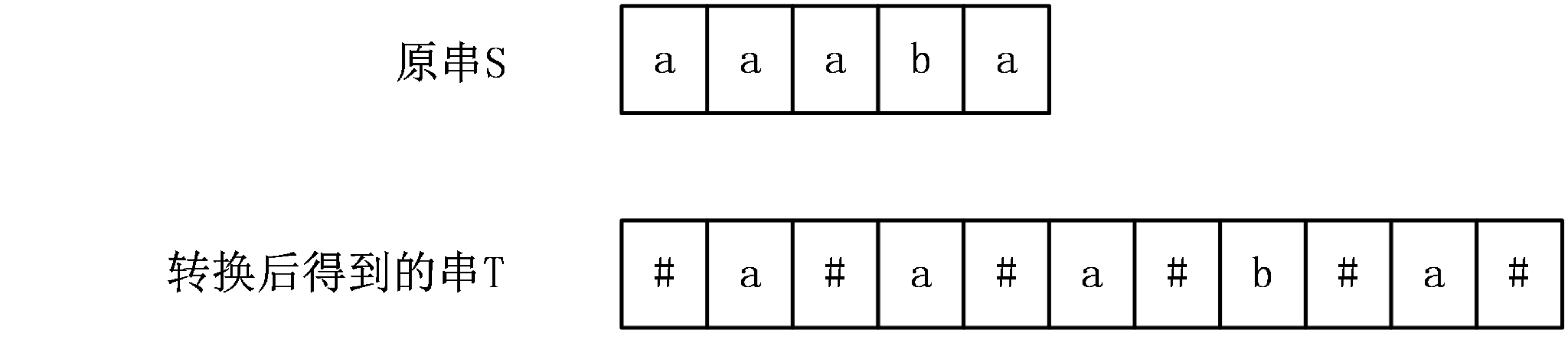
transform

Len数组的计算

从左往右依次计算Len[i]，当计算Len[i]时，Lenj已经计算完毕。设P为之前计算中最长回文子串的右端点的最大值，并且设取得这个最大值的位置为po，分两种情况。

第一种情况：i<=P

找到i相对于po的对称位置，设为j，那么如果Len[j]<P-i

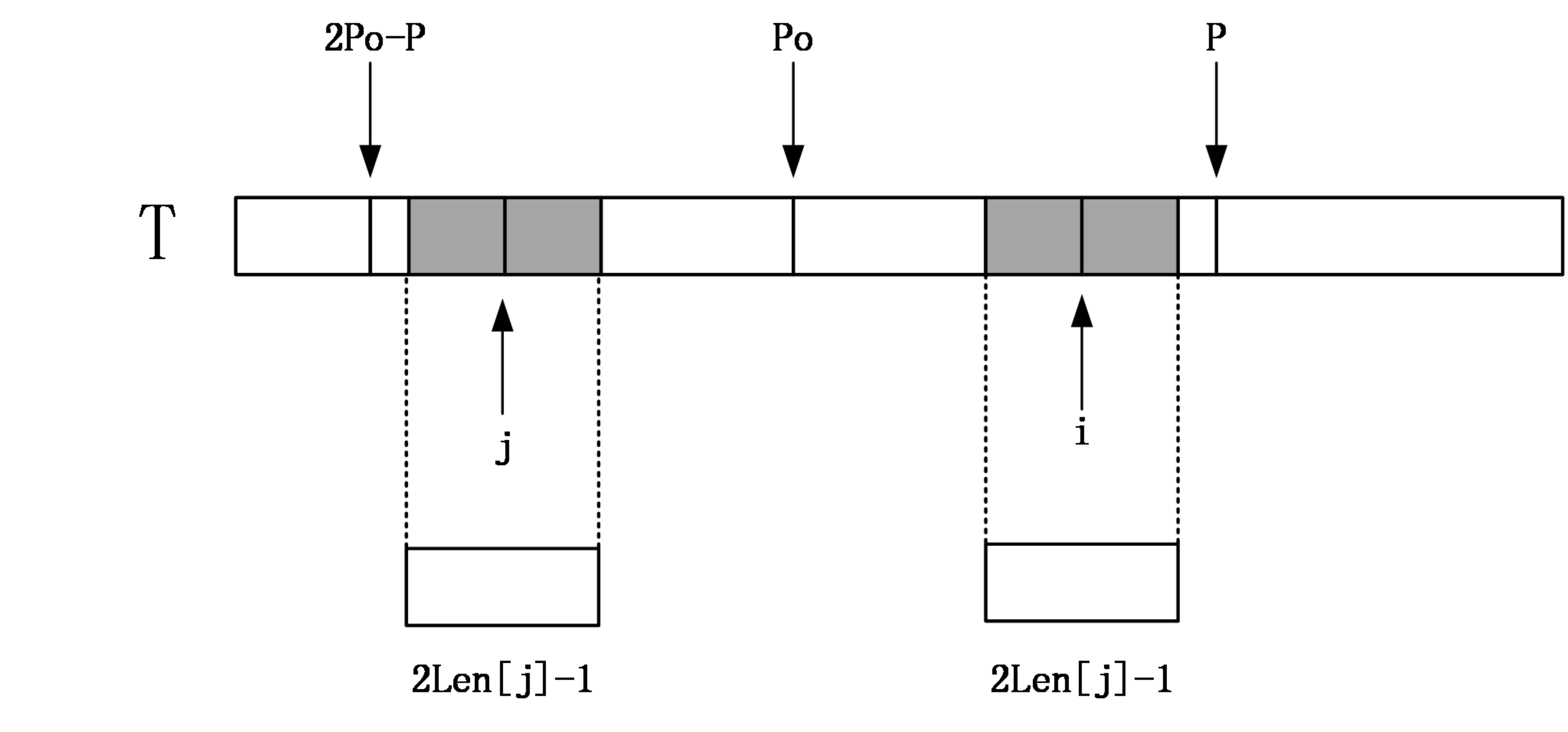
ixiaoyup1

那么说明以j为中心的回文串一定在以po为中心的回文串的内部，且j和i关于位置po对称，由回文串的定义可知，一个回文串反过来还是一个回文串，所以以i为中心的回文串的长度至少和以j为中心的回文串一样，即Len[i]>=Len[j]。因为Len[j]<P-i,所以说i+Len[j]<P。由对称性可知Len[i]=Len[j] 。

如果Len[j]>=P-i,由对称性，说明以i为中心的回文串可能会延伸到P之外，而大于P的部分我们还没有进行匹配，所以要从P+1位置开始一个一个进行匹配，直到发生失配，从而更新P和对应的po以及Len[i]。

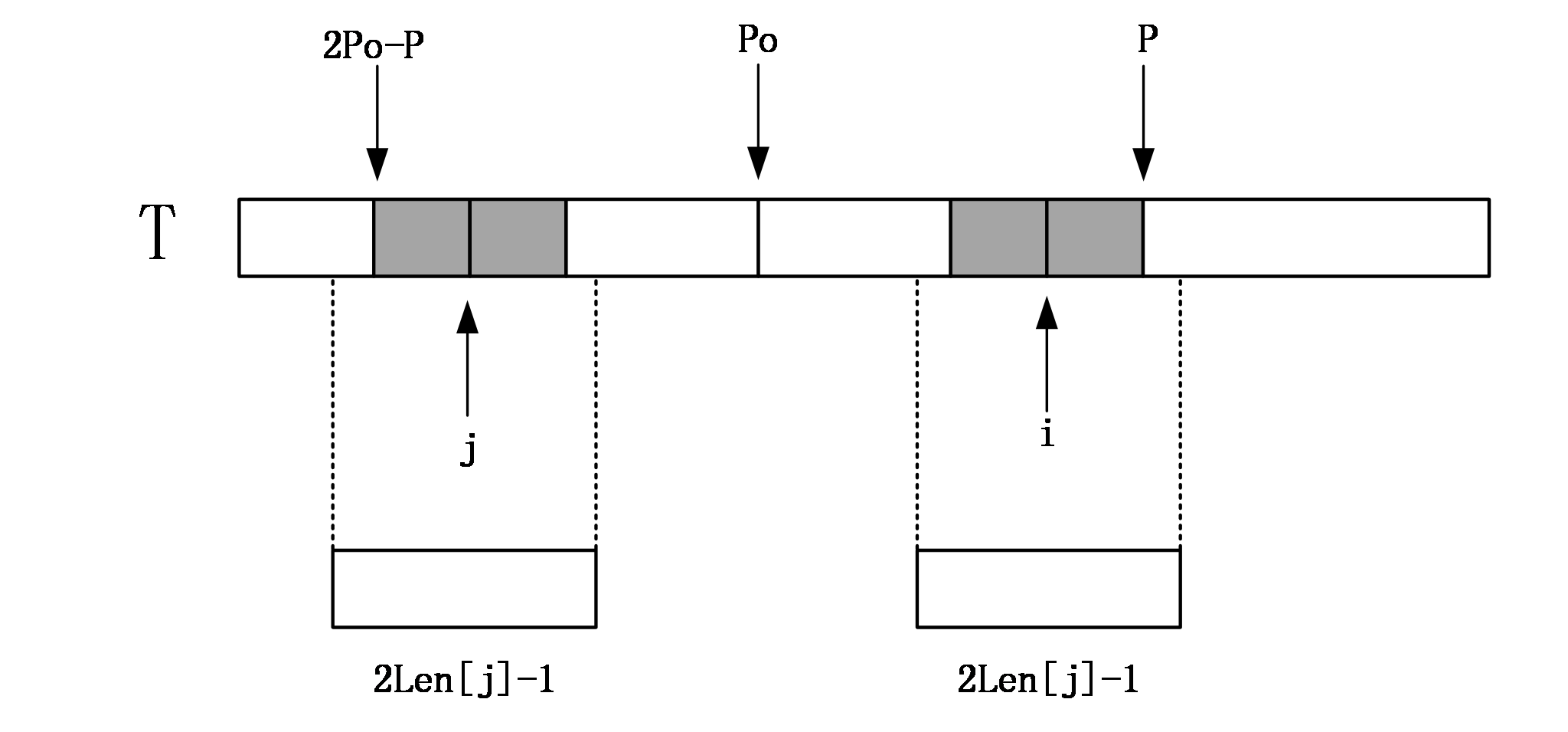
ixiaoyup12

第二种情况: i>P

如果i比P还要大，说明对于中点为i的回文串还一点都没有匹配，这个时候，就只能老老实实地一个一个匹配了，匹配完成后要更新P的位置和对应的po以及Len[i]。

idayup

Python3实现Manacher算法

    def longestPalindrome(self, s: str) -> str:
        s = "@#"+"#".join(s)+"#$"
        mx,ans,p0=0,0,0   ##### 最右边位置，最大长度,中心位置
        Len = [0]*len(s)
        mxstr = ''
        for i in range(len(s)):
            if mx>i:
                Len[i]=min(mx-i,Len[2*p0 - i])
            else:
                Len[i] = 1
            while i+Len[i]<len(s) and   s[i-Len[i]]==s[i+Len[i]]:
                Len[i] += 1
            if Len[i]+i > mx :
                mx=Len[i]+i
                p0 = i
            if Len[i] >= ans:
                mxstr = s[i-Len[i]+1:i+Len[i]] 
                ans=Len[i]

        return  mxstr.replace("#","").replace("$","")