90％的司机认为自己的驾驶水平高于平均水平，90%的人认为自己比人群平均智商要高，而关键是这都是可能符合真实数据的，确实是真实的，并没有造假，然后就认为“哇，其他人在客观地评估自己方面很糟糕”。这时您应该想到的是如果我们使用均值，这听起来并不那么令人难以置信。假如数据分布严重倾斜，是左偏态或者右偏态的话，就会存在严重的误导作用。因为平均值经常会骗人。而很多人却总是使用平均数来骗人显示自己某方面的的优越性，这是不科学的，中位数才是正常情况下的一般水准。 我们来看一个实际例子说明平均数的不可靠，假设

import numpy as np
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import matplotlib

a = np.array([1.0,8.6,8.4,8.7,8.8,8.9,8.9,9.0,9.1])
plt.boxplot(a)

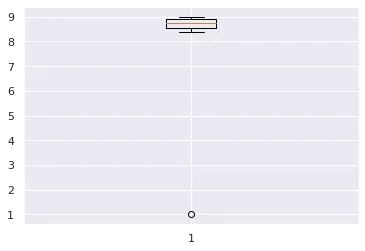
结果是这样的 statistic_out

由于一个异常值就使得数据平均值变化很大，使得其他数值都大于平均值。 区别在于我们是使用平均值还是中位数来表示“平均”司机水平。使用平均值，我们将所有值相加并除以值数，得到的数据集为7.9。由于10位驾驶员中有9位的技能得分高于此，因此90％的驾驶员可以被认为高于平均水平！ 相反，通过从最低到最高对值进行排序并选择一半的数据点较小而一半的数据点较大的值来找到中位数。这是8.8，下面有5个司机，上面有5个司机。根据定义，50％的司机低于中位数，50％的司机超过中位数。如果问题是“您认为自己比其他司机的50％强吗？”超过90％的司机无法如实回答。 （中位数是百分位数（也称为分位数）的特殊情况，该数值是给定百分比的数字较小。中位数是第50个分位数：数据集中50％的数字较小。我们还可以找到第90个分位数，其中90％的值较小；第10个分位数，其中10％的值较小。百分位数是描述数据集的直观方式。）

为何如此重要

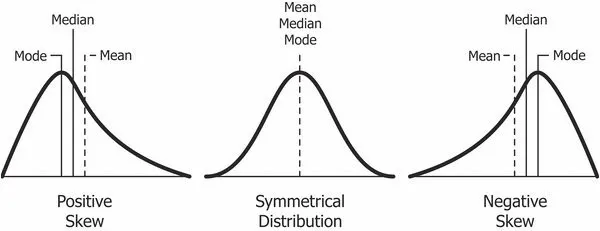
这似乎是人为的例子或技术性的问题，但在现实世界中，经常出现均值和中位数不一致的数据。当值对称分布时，平均值等于中位数。但是，现实世界中的数据集几乎总是带有偏斜的度量，无论是正偏还是负偏（也叫左偏态和右偏态）：

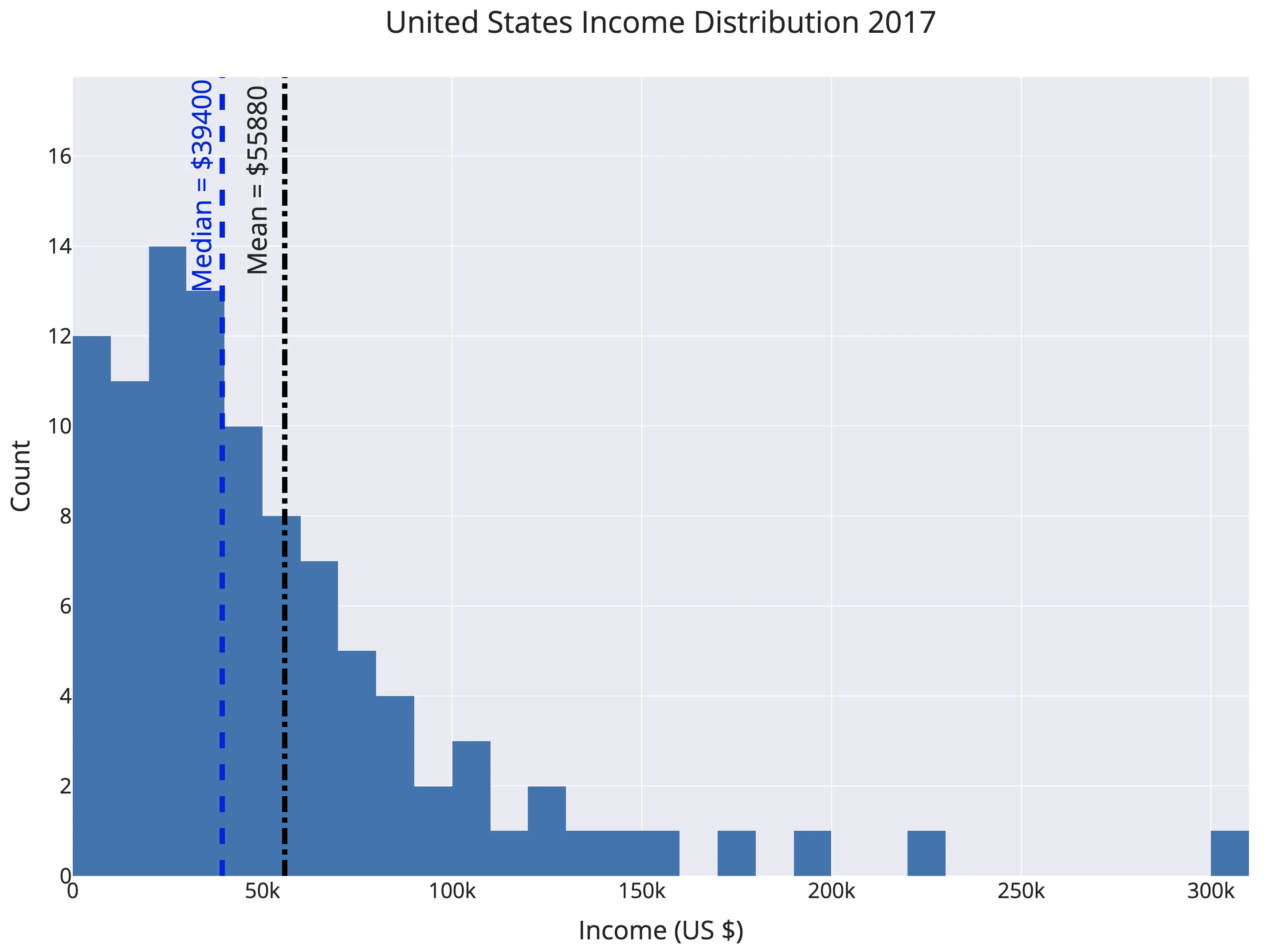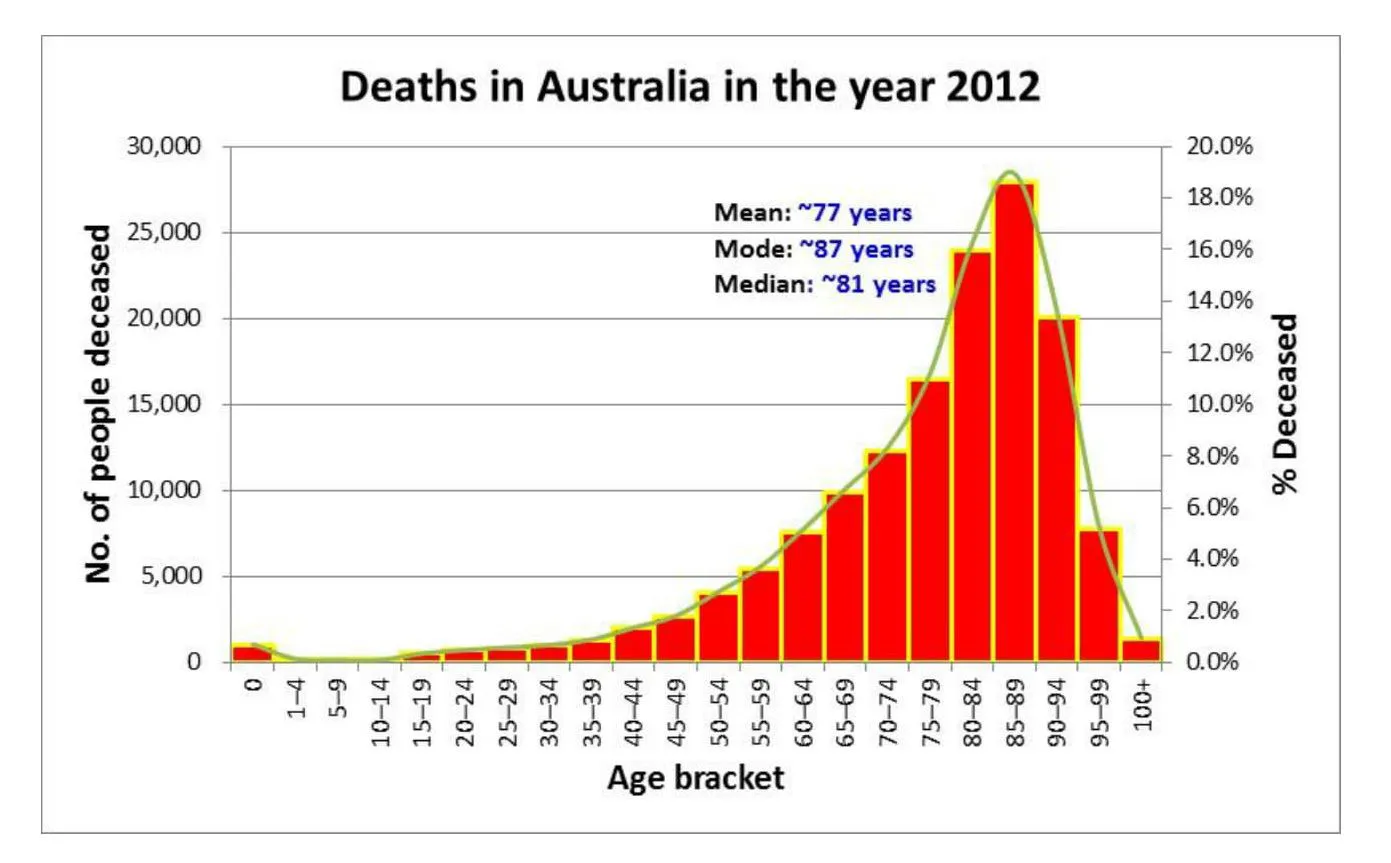
piantai 在正偏分布中，平均值大于中位数。当图形上端的离群值相对较少时，就会向右“偏斜”，而大多数值则聚集在较低值上，从而发生这种情况。现实世界中的情况是个人收入，即平均收入大大高于中位数收入。下图显示了2017年美国收入分布的直方图百分位数。 shouru 总体模式很清楚：一些收入很高的人将图表向右（正）倾斜，使均值超过了中位数。价值55880美元，均值接近66％。解释是66％的美国人的收入低于平均国民收入-当以平均数为平均值时！这种现象几乎在每个国家都有发生。 左偏态的一个示例是死亡年龄。不幸的是，在此数据集中，一些死亡年龄相对较小，降低了均值并使图表向左（负）倾斜。 leftskew

在负偏斜的情况下，中位数大于平均值。结果是，将平均值定义为平均值时，更多的人可以超过“平均值”。“大多数人的寿命比平均寿命长”可能是一个奇怪的标题，但是如果您仔细选择统计数据，您就可以发现。 大多数涉及人类行为的数据集都表现出某种偏差。正所谓“天之道 损有余而补不足 人之道 损不足以奉有余”，股市收益，收入，社交媒体追随者，战死人数和城市规模都是高度扭曲的分布，在这些认为的行为中很多都符合这种偏差。我们人类是在平等和谐的地方发展起来的，那里的所有数据集都是正态分布的，但是现在人类的现代生活被不平等的分布所支配。生活在极端状态中提供了难以置信的回报的机会，但这些回报只会给极少数人带来。这也意味着我们在谈论均值和中位数作为数据集的“平均”表示时必须谨慎。

结论

在统计过程中，时刻提醒自己，当您指定“平均”的时候，您需要弄清楚您是在谈论平均值还是中位数，因为这会有所不同。世界不是对称分布的，因此，我们不应期望分布的均值和中位数相同。 机器学习可能会吸引所有人的注意力，但是数据科学真正重要的部分是我们每天使用的部分：基本统计信息可帮助我们了解世界。能够分辨出平均值和中位数之间的差异似乎有些普通与简单，与知道如何建立神经网络相比，它与我们的日常生活才是真正的息息相关，不要被表面现象所误导，学会从现象看清楚事物的本质。