定义

梯度下降法（Gradient descent）是一个一阶最优化算法，通常也称为最陡下降法。 要使用梯度下降法找到一个函数的局部极小值，必须向函数上当前点对应梯度（或者是近似梯度）的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索，则会接近函数的局部极大值点；这个过程则被称为梯度上升法。

实例展示及梯度下降算法说明

梯度下降一般使用在损失函数中使用，假设y=(x+8)²为某损失函数

import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-20, 4, 0.01)
y = (x + 8)*(x+8)
plt.plot(x,y)
plt.plot([-8,-8],[0,140])

func

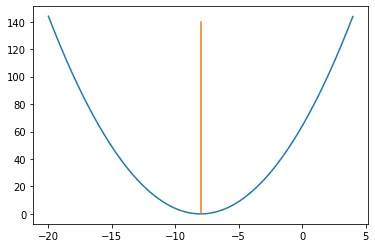
解决方案：仅通过查看图表即可知道答案。当x = -8（即x = -8，y = 0）时，y =（x + 8）²达到最小值。因此，x = -8是函数的局部和全局最小值。 现在，让我们看看如何使用梯度下降来获得相同的数值。

步骤1：初始化x = -3。然后，找到函数的梯度dy / dx = 2 *（x + 8）。

步骤2：朝渐变的负方向移动（为什么？）。但是到底要移动多少呢？为此，我们引入学习率。就是每次调整x的梯度，这里假设学习率→0.01

步骤3：让我们执行2次梯度下降迭代看看

#初始化 x0 = -3, rate = 0.01,dy/dx = 2(x+8)

#第一次迭代
# x1 = x0 - rate*(dy/dx) = -3 - 0.01*(2*(-3+8)) = -3.1
#第二次迭代
# x2 = x1 - rate*(dy/dx) = -3.1 - 0.01*(2*(-3.1+8)) = -3.198

步骤4：我们可以观察到X值正在缓慢减小，并且最终应该收敛到-8（局部最小值）。但是，我们应该执行多少次迭代？

因为算法虽然可以无尽靠近-8，却不能够一直运行下去，因此我们在算法中设置一个精度变量，该变量计算两个连续的“ x”值之间的差，就是x的变化量。如果连续2次迭代的x值之间的差小于我们设置的精度，就停止运算，得出结果。

Python的梯度下降

这里我们使用python的梯度下降找到函数y=(x+8)*(x+8)的最小值

步骤1：初始化数值

initx = -3#算法以x = -3的
rate = 0.01#学习速率
cutoff = 0.000001 #精度，这将告诉我们何时停止算法
previous_step_size = 1#
max_iters = 100000#最大迭代次数
iters = 0 #迭代计数器
df = lambda x:2 *(x + 8)#我们函数的斜率，梯度方向

步骤2：循环并找到最小值


while previous_step_size > cutoff and iters < max_iters:
    prev_x = initx #Store current x value in prev_x
    initx -= rate * df(prev_x) #Grad descent
    previous_step_size = abs(initx - prev_x) #Change in x
    iters = iters+1 #iteration count
    print("迭代次数",iters,"\nX 值为：",initx) #Print iterations
    
print("获得最小值：", initx)

结果

迭代次数 1 
X 值为： -3.1
迭代次数 2 
X 值为： -3.198
迭代次数 3 
X 值为： -3.29404
迭代次数 4 
X 值为： -3.3881592
迭代次数 5 
X 值为： -3.480396016
···
迭代次数 186 
X 值为： -7.883313642475223
迭代次数 187 
X 值为： -7.885647369625718
迭代次数 188 
X 值为： -7.8879344222332035
迭代次数 189 
X 值为： -7.890175733788539
迭代次数 190 
X 值为： -7.892372219112769
迭代次数 191 
X 值为： -7.894524774730513
迭代次数 192 
X 值为： -7.8966342792359026
迭代次数 193 
X 值为： -7.898701593651184
迭代次数 194 
X 值为： -7.900727561778161
····
迭代次数 565 
X 值为： -7.999944830027104
迭代次数 566 
X 值为： -7.999945933426562
迭代次数 567 
X 值为： -7.999947014758031
迭代次数 568 
X 值为： -7.99994807446287
迭代次数 569 
X 值为： -7.999949112973613
迭代次数 570 
X 值为： -7.99995013071414
迭代次数 571 
X 值为： -7.999951128099857
获得最小值 -7.999951128099857

从结果看来,在迭代到194次的时候就到了7.9，而在571次的时候到达目标精度，梯度下降的时候在前面的时候精确度是迅速提高的，而在后面的话就越来越慢了。

总结

本文手把手的从一个二次函数寻找最小值开始，探索如何使用迭代找到函数最小值，这也是神经网络反向传播算法的基础，熟练掌握对于理解神经网络还是有所帮助的。