使用bootstrapping计算置信区间

概念

置信区间(confidence interval,ci)是总体数值在特定可信度下的区间。 它是根据原始观测样本估计的，通常定义为 95%.即通常所说的95%置信区间.

为何使用置信区间

一般情况下,获得的样本都是抽样得到的,总体是未知的,这样从样本中获得的数据没法直接反映总体情况,为了表示样本表示总体的情况,置信区间也就有了用武之地.

置信区间的计算

假设有个正态分布的数据集,标准的正态分布,置信区间对应的zscore为

置信区间  zscore
0.90	1.645
0.95	1.96
0.99	2.58

置信区间计算方法为

也就是平均值加上zscore除以根号n的值为对应置信区间的上限,减去为下限.

应用

说了这么多,其实最重要的还是如何在科研当中或者数据分析当中使用,最近就看到一篇文章使用bootstrapping的方法绘制分布的95%置信区间图.这里就这样一个问题进行演示.

首先是数据的生成

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
np.random.seed(1024)
data_nor = np.random.normal(loc=1,scale=2,size=1000)

查看其累积曲线

通过其和占比画出

x = np.sort(data_nor)
n = len(x)
y = np.arange(1,n+1)/n
plt.plot(x,y,marker='.',linestyle="none")
plt.xlabel("x")
plt.ylabel("percentage")
plt.title("CDF")
plt.savefig("cdf.png",dpi=200)
plt.close()

绘制得到的图形为:

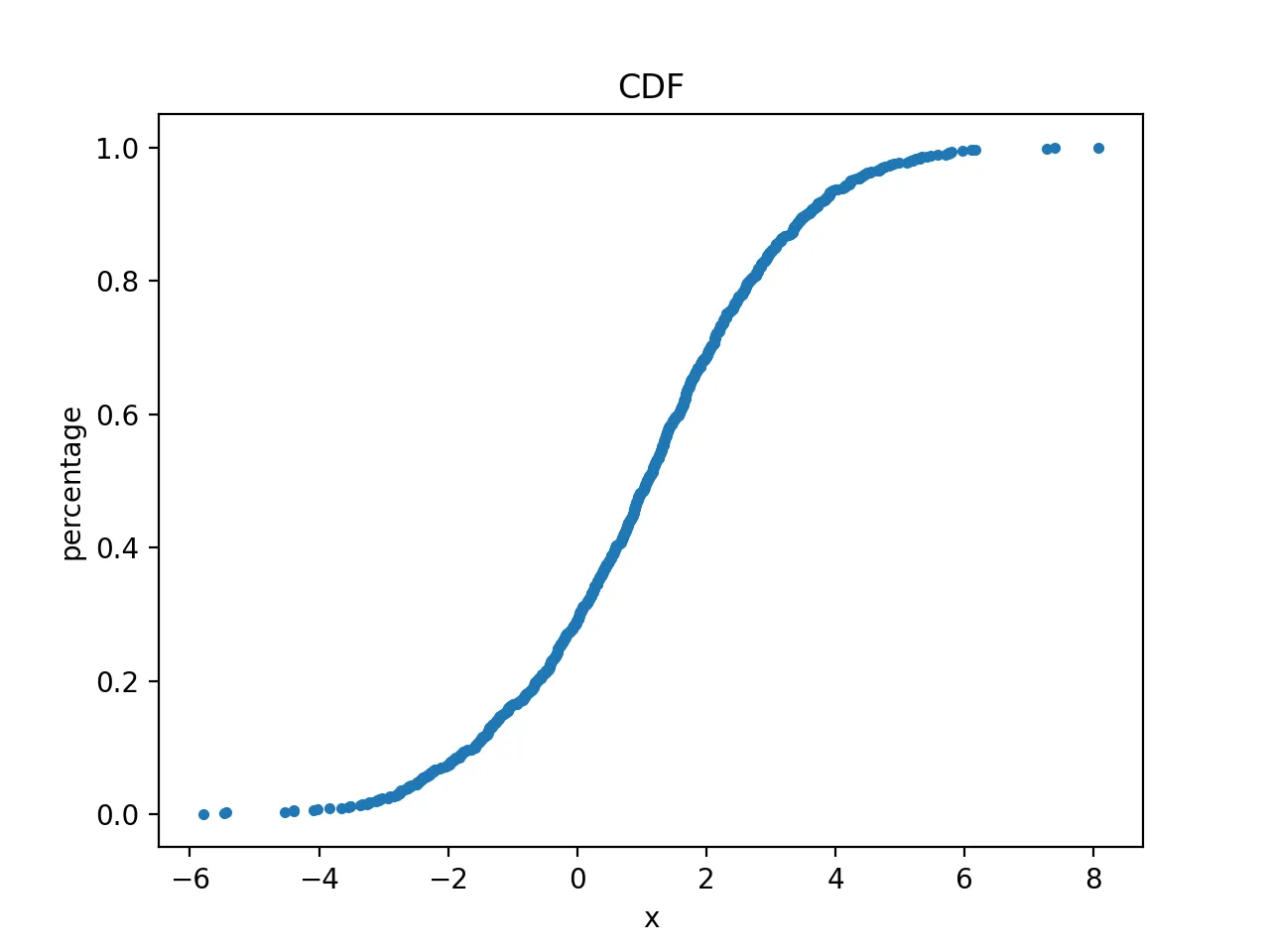
查看其密度曲线

统计值光滑后的曲线

sns.distplot(data_nor,hist=False)
plt.xlabel("x")
plt.ylabel("PDF")
plt.title("PDF plot")
plt.savefig("pdf.png",dpi=200)
plt.close()

其图形为:

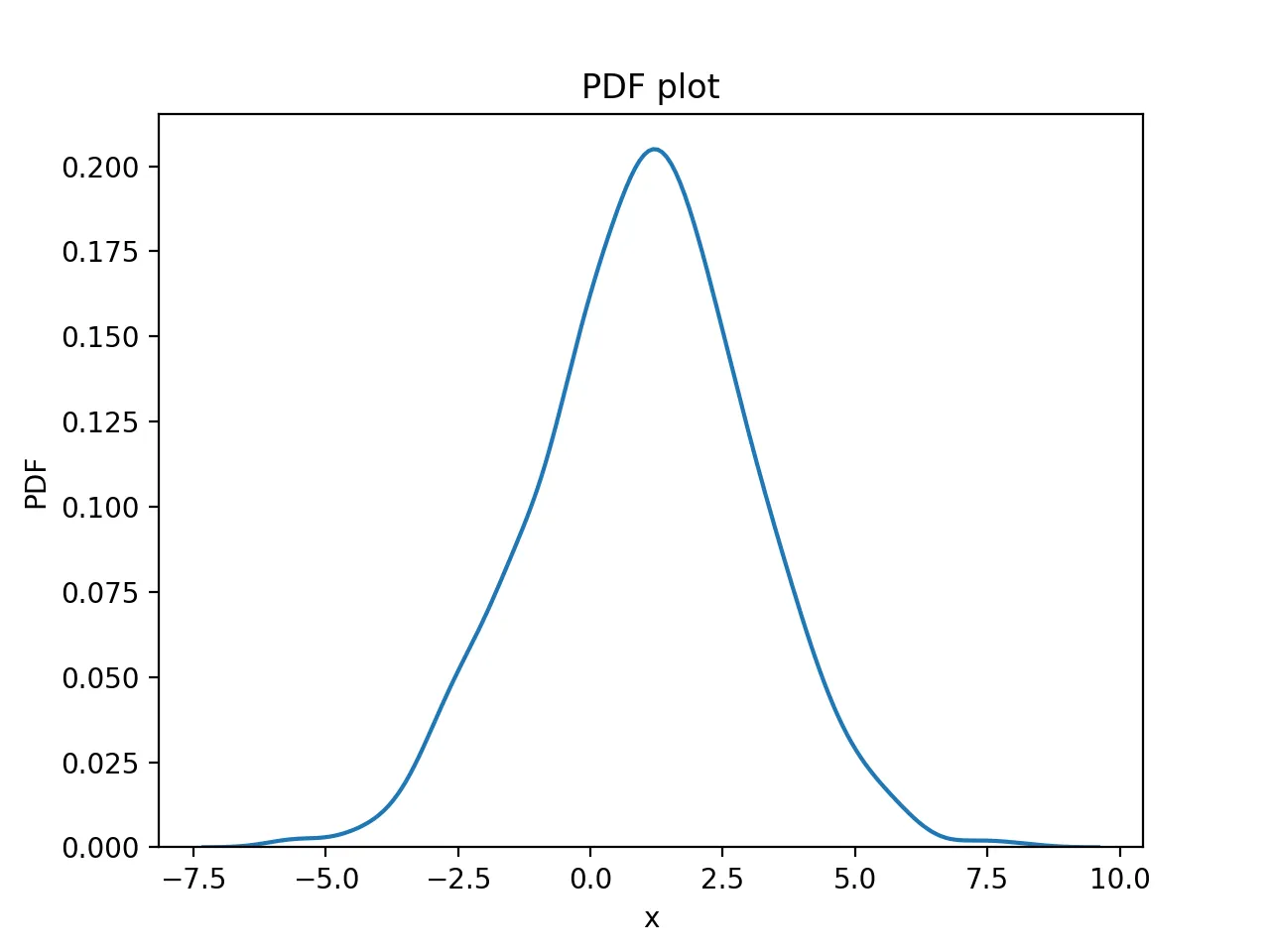
通过bootstrapping随机生成背景数据并计算置信区间

通过对data_nor随机抽取100个数值,重复10000次后得到其置信区间,通过使随机抽取的数据设置透明达到突出原始数据并绘制随机抽取的数据并计算置信区间

# 首先绘制原始数据作为中间曲线`
plt.plot(x,y,marker='.',linestyle="none")
bs_mean = []
for i inrange(10000):
    bs_sample = np.random.choice(data_nor,size=100)
    x = np.sort(bs_sample)
    bs_mean.append(np.mean(x))
    n = len(x)
    y = np.arange(1,n+1)/n
    plt.scatter(x,y,s=1,marker='.',alpha=0.2)
plt.savefig("bs.png",dpi=200)
plt.close()

绘制得到的图形为:

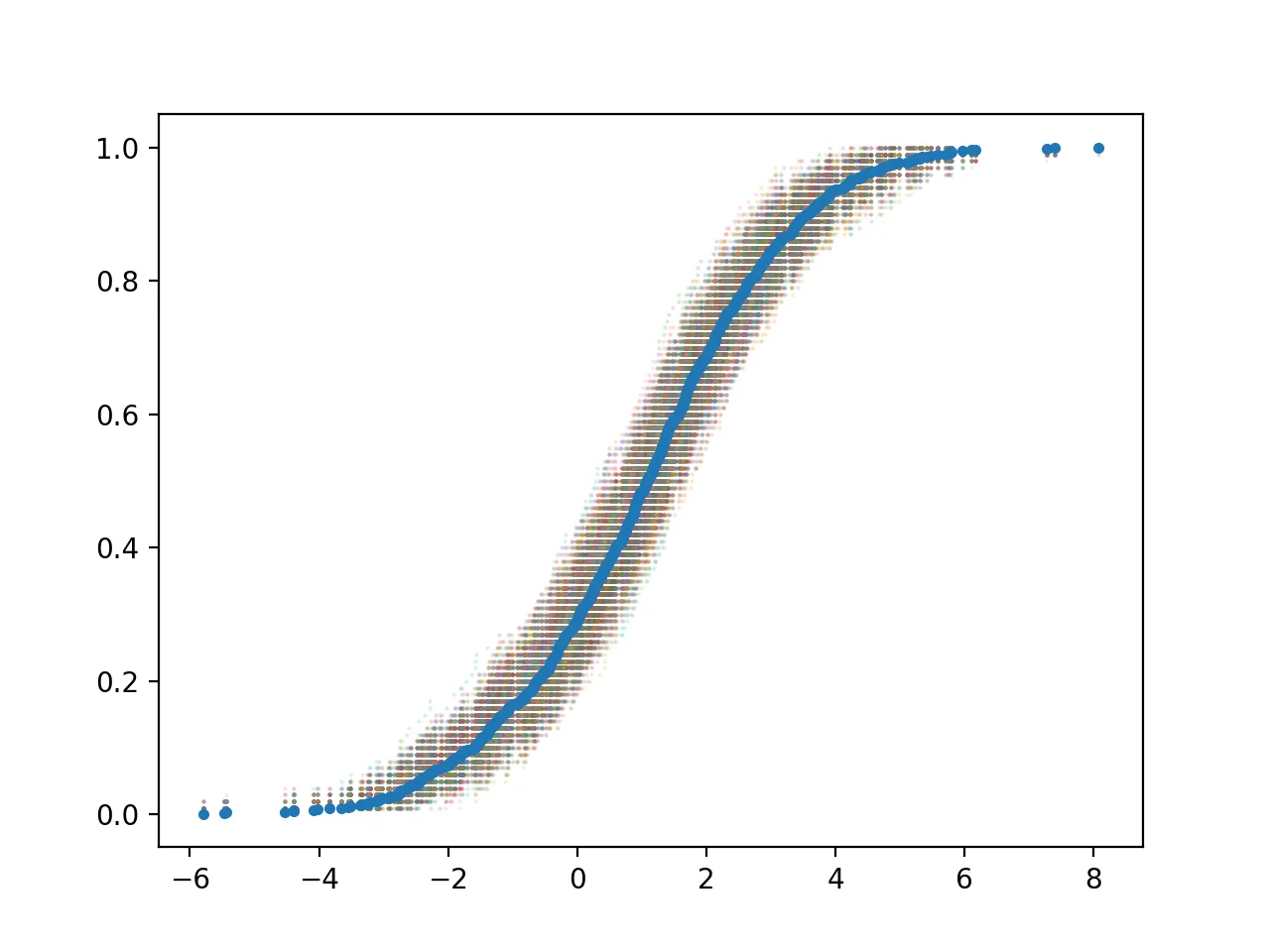
bootstrapping后的数据均值的分布图并通过直线标识2.5与97.5的置信区间 置信区间可直接通过np.percentile计算得到

plt.hist(bs_sample,bins=0.1,density=True)
plt.axvline(x=np.percentile(bs_sample,[2.5]), ymin=0, ymax=1,label='2.5%',c='y')
plt.axvline(x=np.percentile(bs_sample,[97.5]), ymin=0, ymax=1,label='97.5%',c='r')
plt.xlabel("x")
plt.ylabel("PDF")
plt.title("BS PDF")
plt.savefig("percent.png",dpi=200)
plt.close()

图形为:

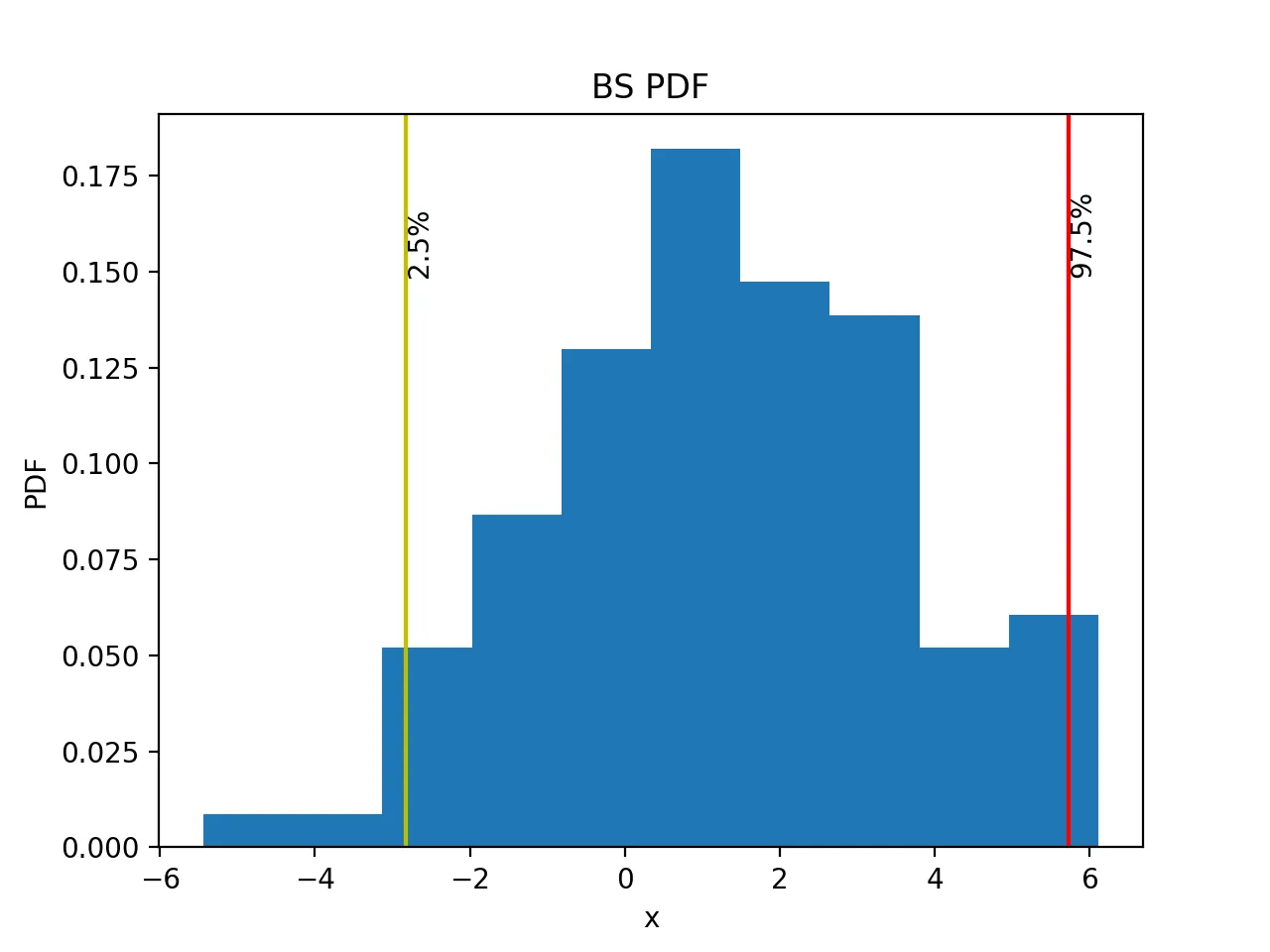
而其95%置信区间为(-2.67366335,4.18761485)

总结

本文介绍了置信区间以及如何通过bootstrapping的方式绘制背景数据并计算其置信区间.