基尼系数和洛伦兹曲线，在表示数据的不平均方面特别是财富的不平均上被广泛应用。但是目前在python里面并没有找到很好的可以直接绘制洛伦兹曲线的函数，由于目前项目用到，也就在实际应用中使用到，就把如何使用numpy，pandas，matplotlib等包来计算基尼系数和绘制洛伦兹曲线的过程记录下来。方便大家遇到相似问题直接使用就可。

本文主要包含如下几个部分：

    1. 样本数据获取
    1. 基尼系数计算
    1. 洛伦兹曲线绘制

1. 样本数据获取

你可以使用pd.read_csv读取已有csv文件中的表格数据，也可以使用本文通过随机产生的一些数据验证一下，这里我们采用numpy自带的随机函数np.random.randint得到数据。 代码如下：

#! env python

## 先导入必要的包
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

## 随机1000 个数据
np.random.seed(1) #种子只是为了重现结果
data = np.random.randint(low = 1, high = 100, size = 1000)#产生1到100的1000个数据

利用numpy的randint方法产生了1000个数据并保存到data数组当中，这里使用seed种子主要是为了大家可以重复出结果

2. 基尼系数计算

那么假设一个群体数据为data的话，基尼系数如何计算呢，这里查看维基百科可以看到计算方法为

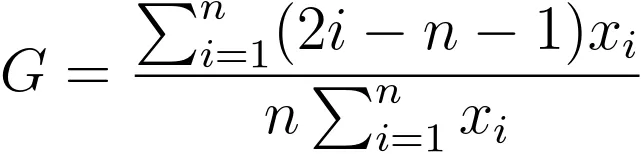
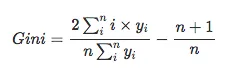
gini_coef 通过变换简化计算 gini_trans 这样右边转化为一个常数，左边可以通过numpy计算，直接上计算基尼系数的函数

def gini(arr):
    # 首先排序
    arr = np.array(sorted(arr))
    
    n = len(arr)
    coef_ = 2. / n
    const_ = (n + 1.) / n
    weighted_sum = sum([(i+1)*yi for i, yi in enumerate(arr)])
    return coef_*weighted_sum/(arr.sum()) - const_

print(gini(data))

#0.3313838956962638

可以看到结果计算出来为0.33 接下来就是如何绘制洛伦兹曲线了

3. 洛伦兹曲线绘制

洛伦兹曲线最初被用于表示收入的不平等参数，曲线上的每个点表示当前百分比的人数占据总财富的百分比比例。其中很著名的80-20理论说明的就是80%的人只占据总财富的20%，还有80%的财富被20%的人占有。跟基尼系数相比，洛伦兹曲线表示的更加详细，可以看到每个点的人员占据的财富比。在洛伦兹曲线中，基尼系数可以看作是曲线与45%线的一个区域大小。为了绘制洛伦兹曲线我们需要添加0，0作为曲线起点。

python洛伦兹曲线绘制函数代码：

def lorenz_curve(X):
    X = np.array(sorted(X))
    X_lorenz = X.cumsum() / X.sum()
    X_lorenz = np.insert(X_lorenz, 0, 0)
    X_lorenz[0], X_lorenz[-1]
    fig, ax = plt.subplots(figsize=[6,6])
    ## 散点图
    ax.scatter(np.arange(X_lorenz.size)/(X_lorenz.size-1), X_lorenz,
               marker='x', color='darkgreen', s=1)
    #
    ax.plot([0,1], [0,1], color='k')
    保存图片
    plt.savefig('luolunzi.png')

绘制结果

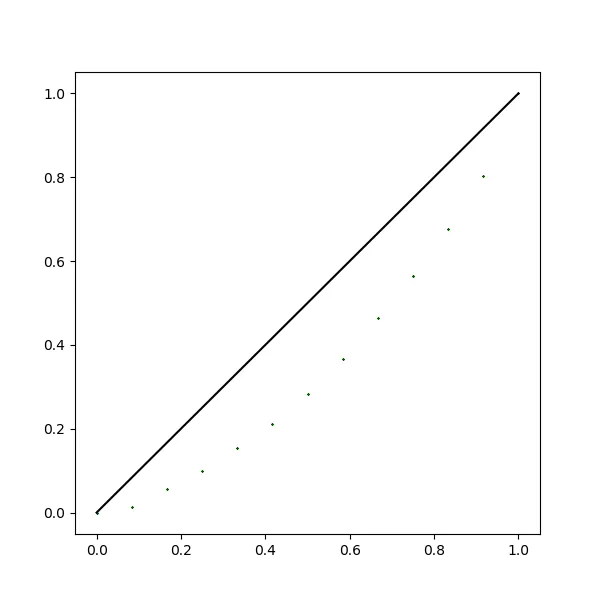
luolunzi

总结

本文介绍数据不平均的一种表示方法，使用到了基尼系数和洛伦兹曲线来表示，并使用python语言实现了基尼系数定义上的计算，并使用绘图工具matplotlib绘制了洛伦兹曲线。